斜視図（等角図）の描き方

等角図の描き方について、基本を分かりやすくご説明いたします。

斜視図、立体図、ポンチ絵、スケッチの基本となるものです。

本ページの解説動画：斜視図（等角図）の描き方【動画】

等角図とは？

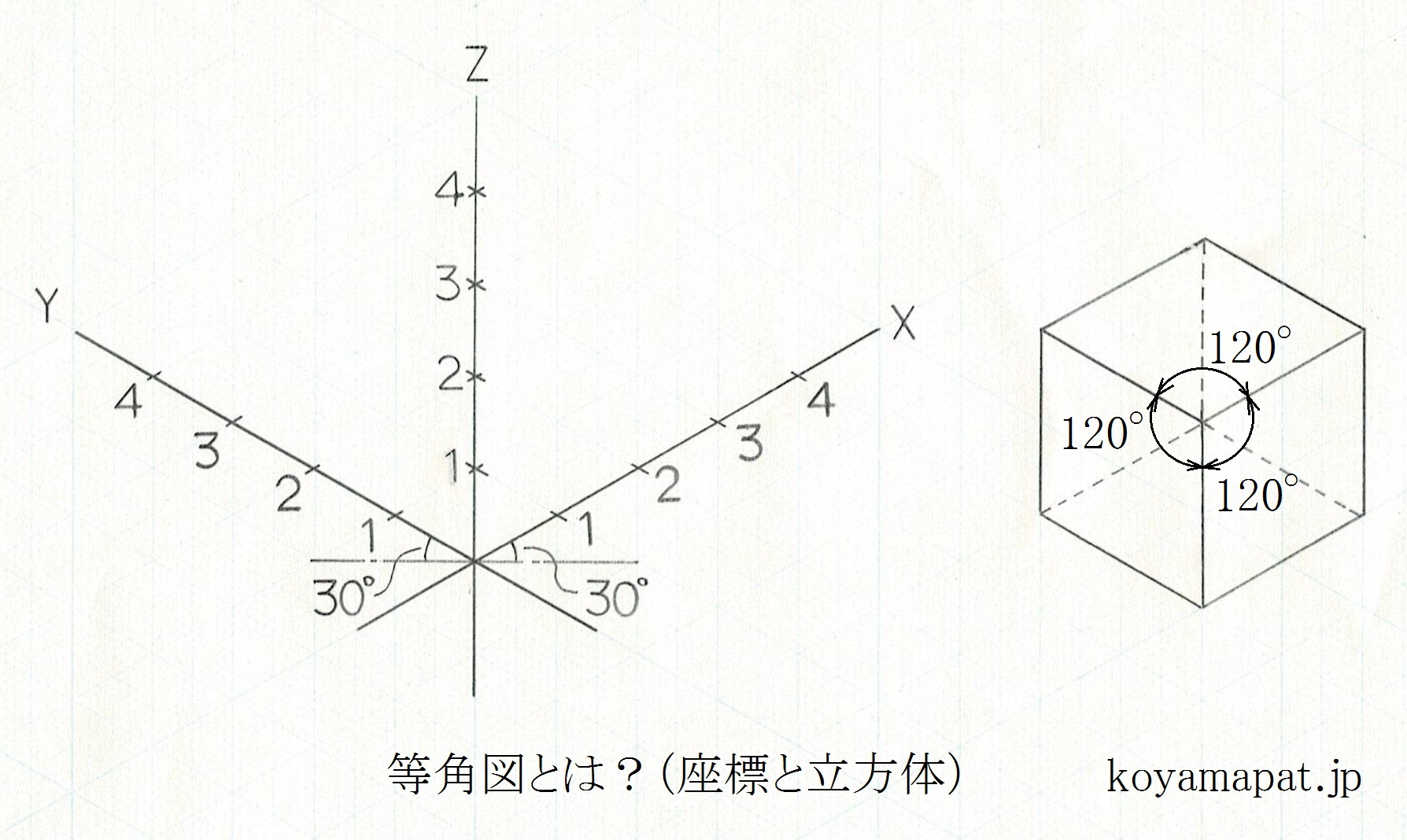
等角図とは？（座標と立方体）

等角図とは、物体を斜め上方等から見た斜視図であり、前後、左右、上下の３本の座標軸（等角軸）が互いに等角（１２０度）で配置された図で、かつ等角軸の軸方向寸法を実寸とした図をいいます。

等角図は、等測図とも呼ばれます。

等角図（等測図）と似たものに、等角投影図（等測投影図）というものがあります。等角図は、等角軸の軸方向寸法を実寸（実長）としますが、等角投影図は、実寸の0.82倍（√２／√３）とします。そのため、両者の違いは、大きさの違いです。詳しくは、「等角図と等角投影図」をご覧ください。

上図から分かるように、Ｘ軸とＹ軸とは、水平線に対し３０度の傾きで配置されます。また、Ｚ軸は、水平線に対し垂直に配置されます。等角図では、等角軸の軸方向寸法を実寸としますから、上図において、原点から各軸の「１」と記載した箇所までの距離は１ｃｍ、「２」と記載した箇所までの距離は２ｃｍとなっています。

なお、「原点」とは、Ｘ軸、Ｙ軸、Ｚ軸の交点をいいます。つまり、ＸもＹもＺも、いずれも０の位置が「原点」です。

等角図と不等角図

等角投影図（等角図）と不等角投影図（不等角図）

なぜ「等角図」というのでしょうか？
どこが「等角」なのでしょうか？

等角投影図（等角図）と不等角投影図（不等角図）との違いを確認してみます。

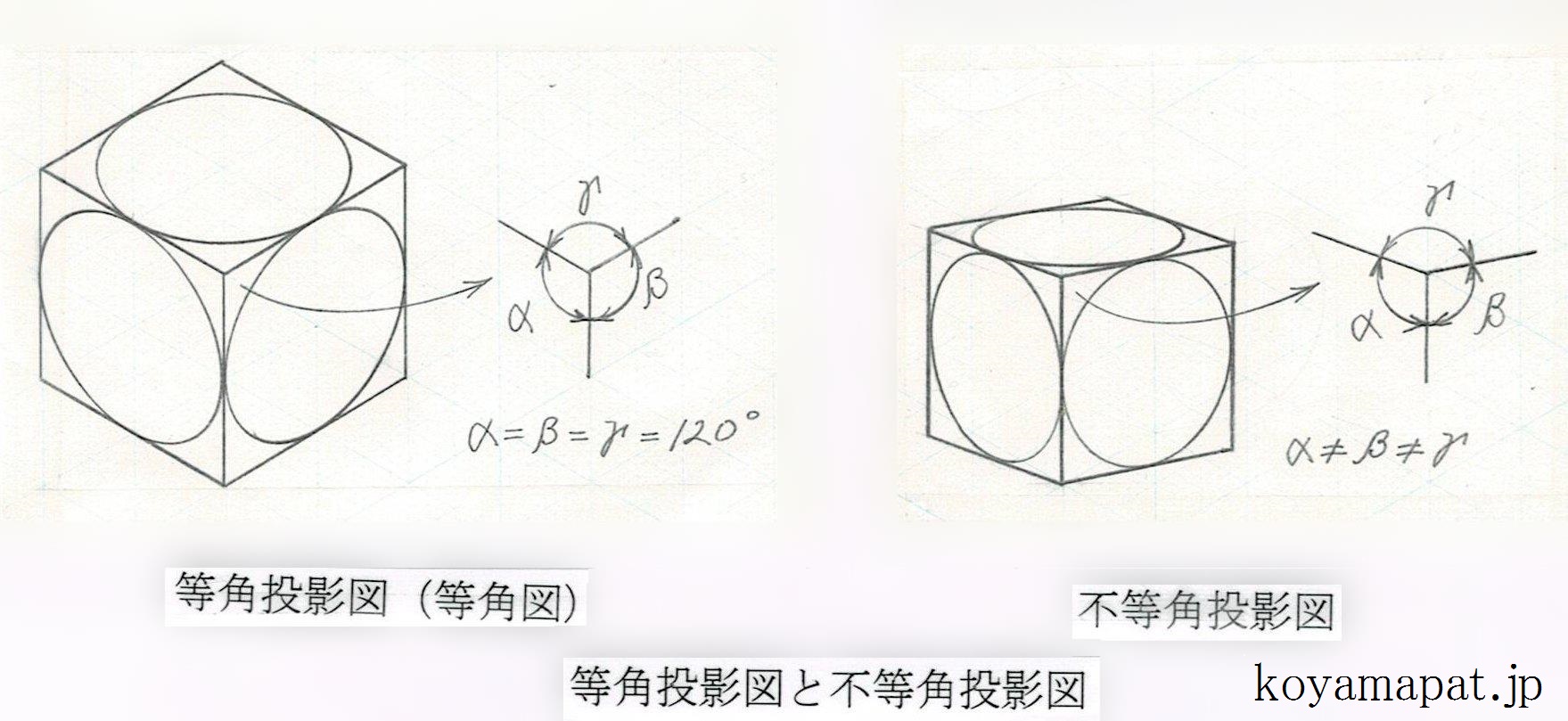
上図から分かるように、等角投影図（等角図）で立方体を描いた場合、手前側の上方角部をみると、隣接する二辺でなす角α（アルファ）、β（ベータ）、γ（ガンマ）は、いずれも１２０度となっています。これら角度α、β、γが、互いに等しい角、つまり「等角」だから、「等角投影図（等角図）」という訳です。

一方、不等角投影図（不等角図）の場合、α、β、γは、互いに異なります。これらα、β、γは、物体を見る角度によって、様々な角度をとることになります。その内、α、β、γを１２０度としたものが等角投影図（等角図）になります。

等角図の描き方

立方体

一辺が２ｃｍの立方体を描いてみます。

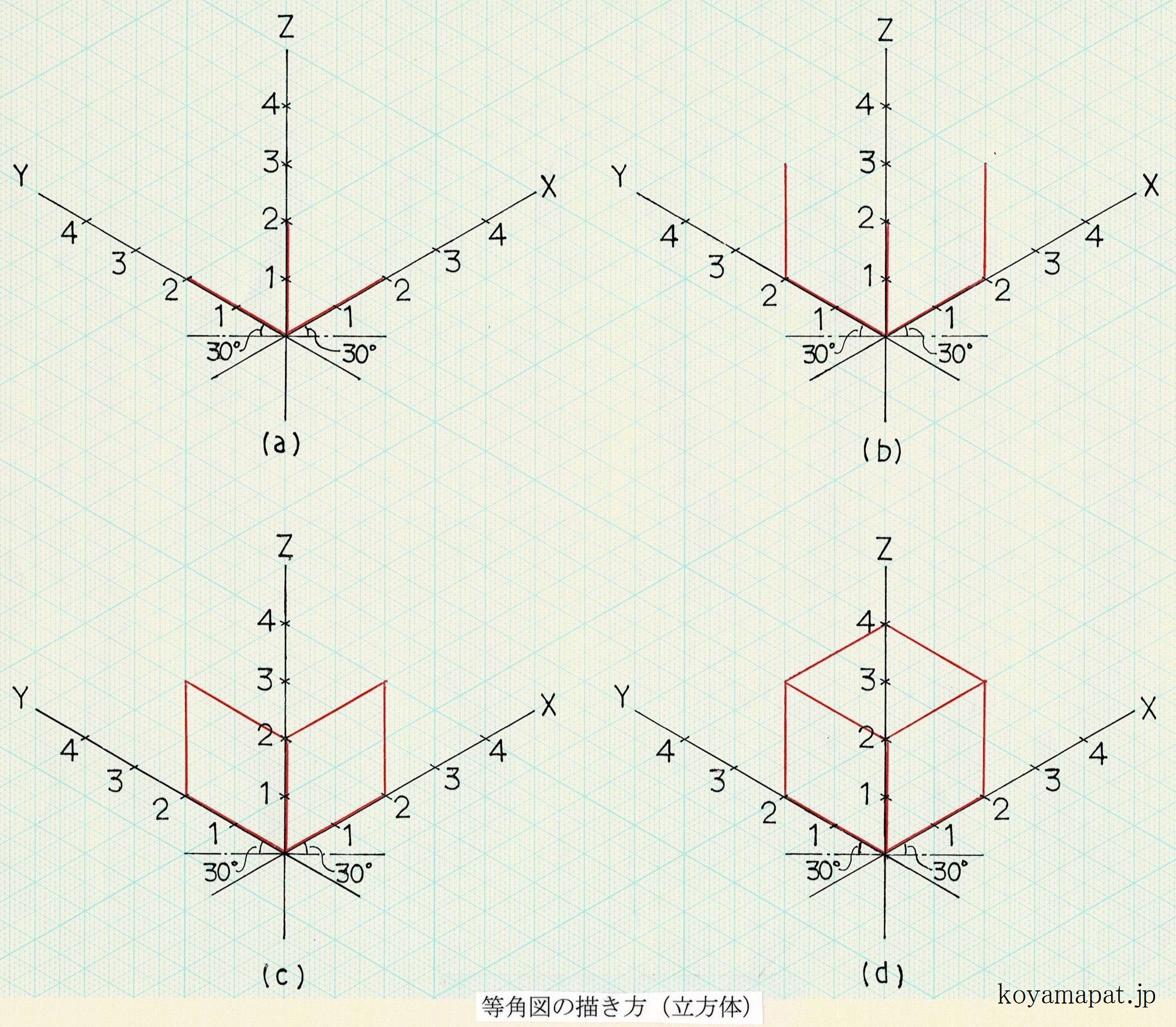
等角図の描き方（立方体）

（ａ）原点から、Ｘ軸方向に２ｃｍ、Ｙ軸方向に２ｃｍ、Ｚ軸方向に２ｃｍだけ、線を引きます。

（ｂ）Ｘが２の位置と、Ｙが２の位置から、それぞれ上方へ（つまりＺ軸と平行に）２ｃｍだけ、線を引きます。

（ｃ）いま引き終えたＸが２の位置から上方へ２ｃｍの線の上端と、Ｚが２の位置とを線でつなぎます。この線は、Ｘ軸と平行な線となります。同様に、Ｙが２の位置から上方へ２ｃｍの線の上端と、Ｚが２の位置とを線でつなぎます。この線は、Ｙ軸と平行な線となります。

（ｄ）いま引き終えた各線と平行に、残りの線を描き、立方体は完成です。

直方体とその応用

縦３ｃｍ、横２ｃｍ、高さ２ｃｍの直方体を描いてみます。

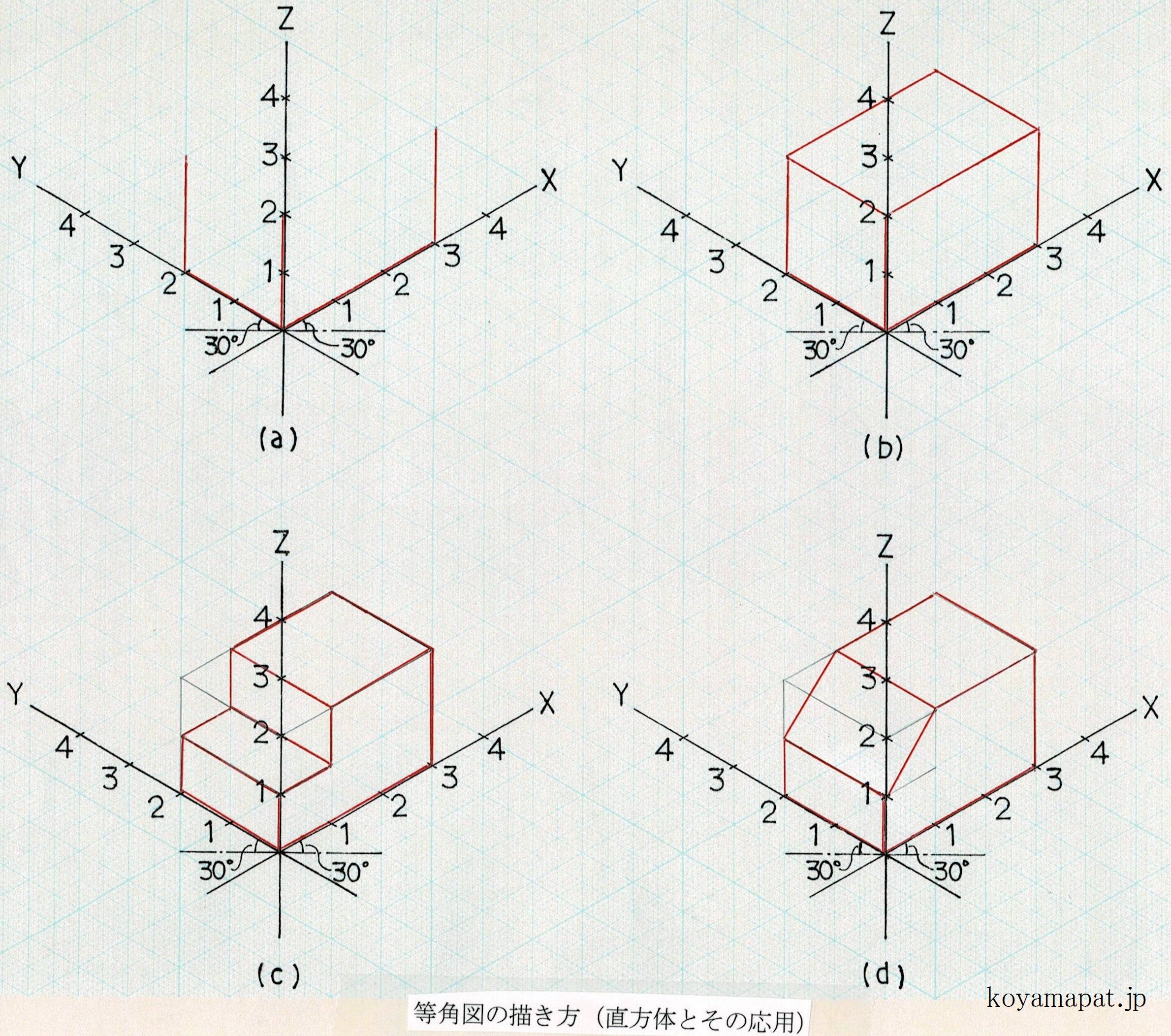
等角図の描き方（直方体とその応用）

（ａ）原点から、Ｘ軸方向に３ｃｍ、Ｙ軸方向に２ｃｍ、Ｚ軸方向に２ｃｍだけ、線を引きます。また、Ｘが３の位置と、Ｙが２の位置から、それぞれ上方へ（つまりＺ軸と平行に）２ｃｍだけ、線を引きます。

（ｂ）残りの線を、Ｘ軸に平行な線と、Ｙ軸に平行な線とでつないで、直方体は完成です。

（ｃ）直方体の応用として、一部に段差を付けることもできます。各点の座標が分かれば、より複雑な図形も描けます。

（ｄ）直方体の応用として、一部に傾斜面を付けることもできます。

円柱

直径２ｃｍ、高さ３ｃｍの円柱を描いてみます。

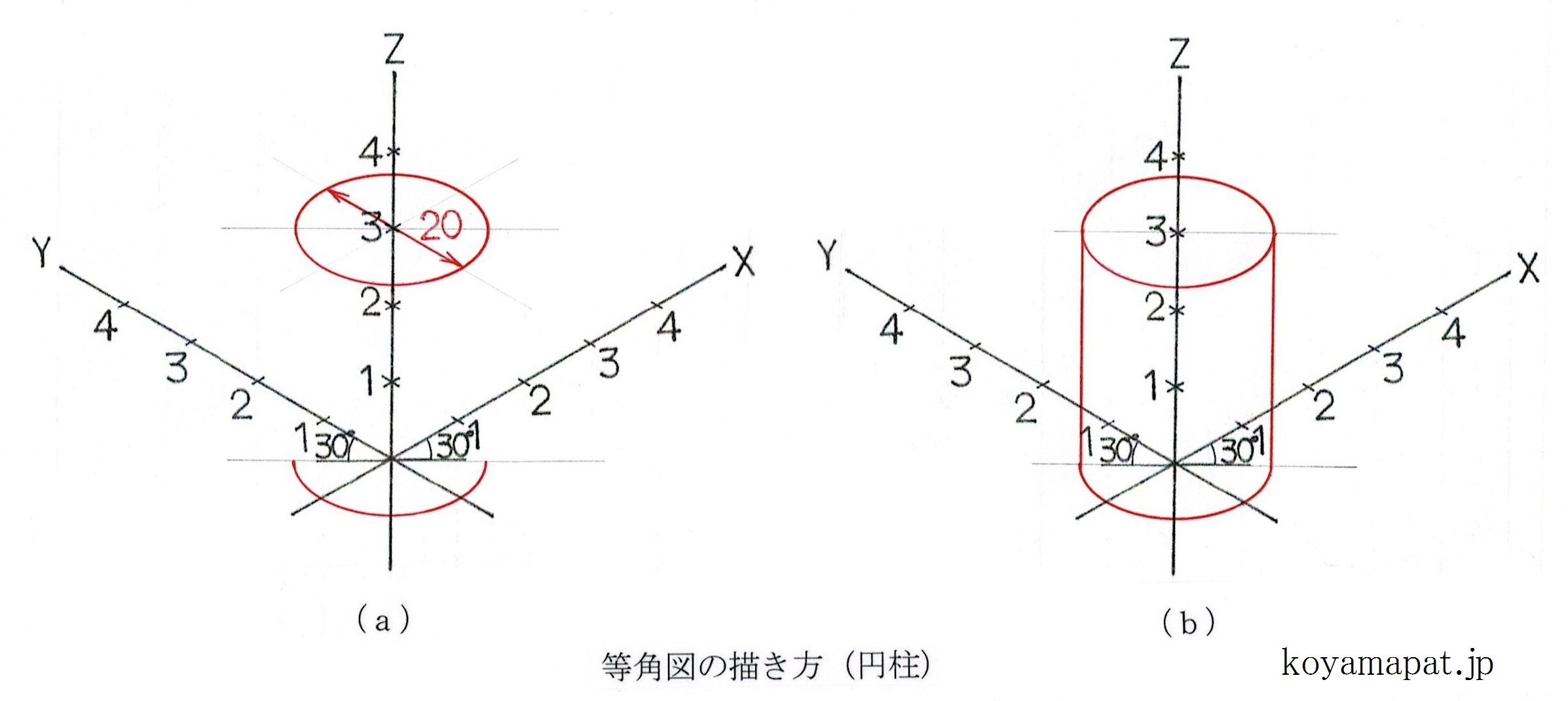
等角図の描き方（円柱）

（ａ）円柱の高さとして、原点と、原点からＺ軸方向に３ｃｍの箇所に、それぞれ水平線（またはＸ軸やＹ軸に平行な線）を引きます。円柱の下面と上面の高さ位置です。そして、それぞれの箇所で、直径２ｃｍ（図面中では２０ｍｍと表示）の上下面を描きます。等角図では、物体を斜め上方から見る関係上、円ではなく、「楕円（だ円）」となります。等角図の場合、３５度の楕円が用いられます。ここでは、直径２ｃｍですから、斜軸（Ｘ軸・Ｙ軸）の軸方向長さが２ｃｍとなる楕円を用います。等角図では、長軸や短軸ではなく、斜軸の方向（Ｘ軸方向やＹ軸方向）の長さで、楕円の大きさを決めます。底面の楕円は、手前側半分しか見えませんから、半周分だけで大丈夫です。

楕円を描くには、楕円定規（テンプレート）を用いるのが便利ですが、楕円定規がなくても、コンパスで近似楕円を描くこともできます（コンパスによる楕円の描き方）。

なお、仮に、円柱を真上から見る場合、水平面に対し９０度の位置から見ることになり、楕円度は９０度となります。９０度の楕円が通常の円です。これに対し、等角図では、楕円度３５度（厳密には３５度１６分）となります。楕円度が９０に近づくほど、丸形（円形）となり、０に近づくほど、細長くなる（線に近づく）ことになります。

（ｂ）上下の各楕円を、Ｚ軸に平行な線でつないで、円柱は完成です。

【補足】楕円の長軸・短軸・斜軸とは？

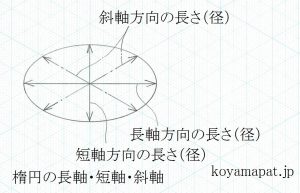
楕円の長軸・短軸・斜軸

楕円の長軸とは、楕円の長手方向をいいます。楕円の長径とは、長軸方向の長さ（径）をいいます。
楕円の短軸とは、楕円の短手方向をいいます。楕円の短径とは、短軸方向の長さ（径）をいいます。
楕円の斜軸とは、楕円の中心を通る線の内、傾斜した等角軸（上図において水平線に対し３０度の傾きの線）の方向をいいます。なお、等角軸については、前記「等角図とは？」をご覧ください。

円錐

底面の直径が２ｃｍ、高さが３ｃｍの円錐を描いてみます。

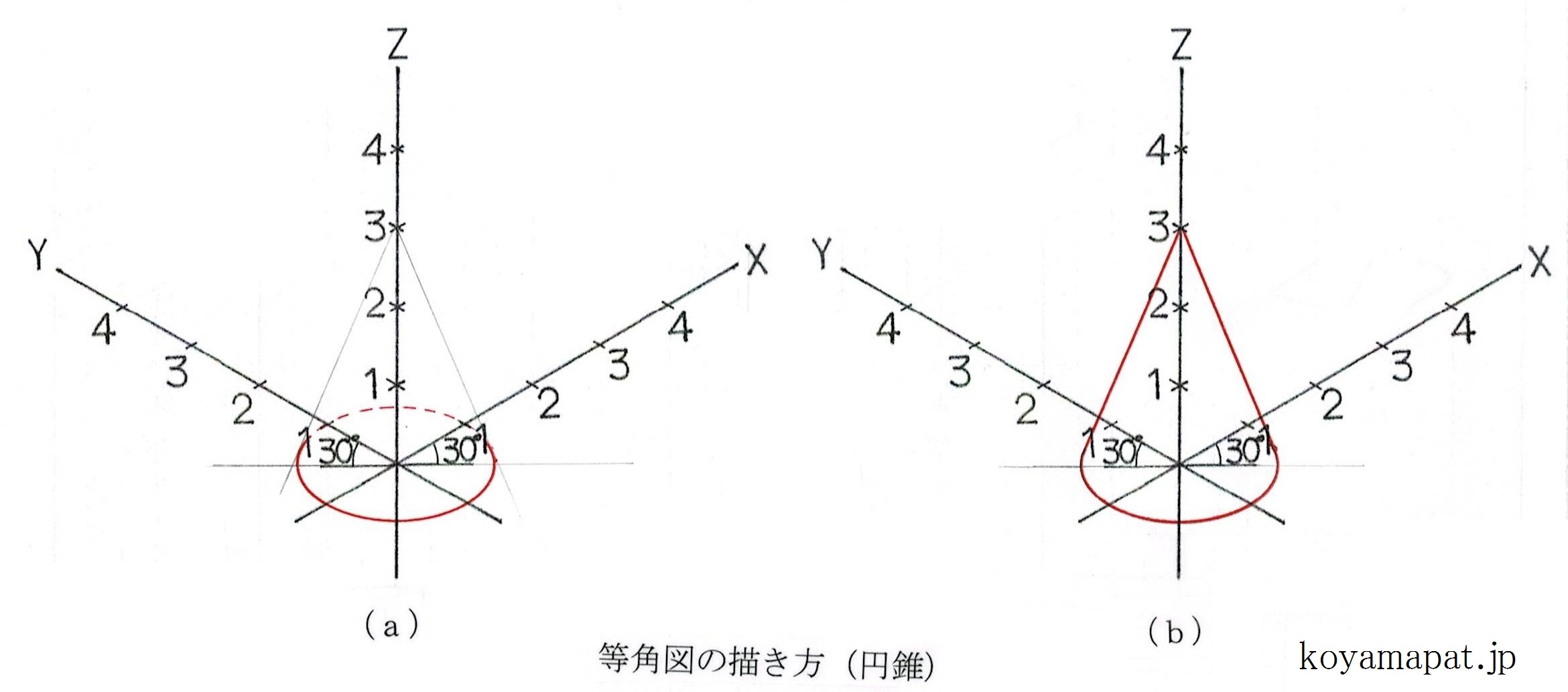
等角図の描き方（円錐）

（ａ）円錐の高さは、Ｚ軸上の原点と、原点から３ｃｍとの位置になります。底面は、直径２ｃｍの楕円となります。３５度の楕円で、且つ、斜軸（Ｘ軸・Ｙ軸）の軸方向長さが２ｃｍとなる楕円を用います。上図の（ａ）から分かるように、楕円がＸ軸上の１（および－１）と、Ｙ軸上の１（および－１）とを通過します。

（ｂ）円錐の頂点（Ｚが３の位置）と、前記楕円とを「接線で」つないで、円錐は完成です。

球

直径２ｃｍの球を描いてみます。

等角図の描き方（球）

球は、どこから見ても形は変わらないので、通常の円となります。但し、等角図の場合、実寸の1.22倍（√３／√２）で描きます。ここでは、直径２ｃｍの球を描こうとしていますから、直径が2.44ｃｍ（２×1.22）の円を描きます。

等角図は、物体を斜め上方から見た図となります。この場合、前記立方体の各辺の寸法などは、本来は実寸よりも小さく（つまり等角図ではなく等角投影図のように0.82倍（√２／√３）で）描くべきとなります。ところが、図面作成の便宜上、等角図では、これら寸法を実寸とする関係で、どこから見ても形状（大きさ）の変わらない球は、逆に1.22倍（√３／√２）します。

なお、等角図で、直径２ｃｍの円（球ではなく円板）を描く場合、斜軸（Ｘ軸・Ｙ軸）の寸法を２ｃｍとする楕円を用いますが、その楕円の長軸寸法は、斜軸寸法の1.22倍（2.44ｃｍ）となり、これは球を描く場合の直径と一致します。詳しくは、等角図と等角投影図（等角図と等角投影図との違いの図）をご覧ください。

段付き棒、円筒、四角錐

いままでの知識を組み合わせて、段付き棒、円筒、四角錐なども描くことができます。

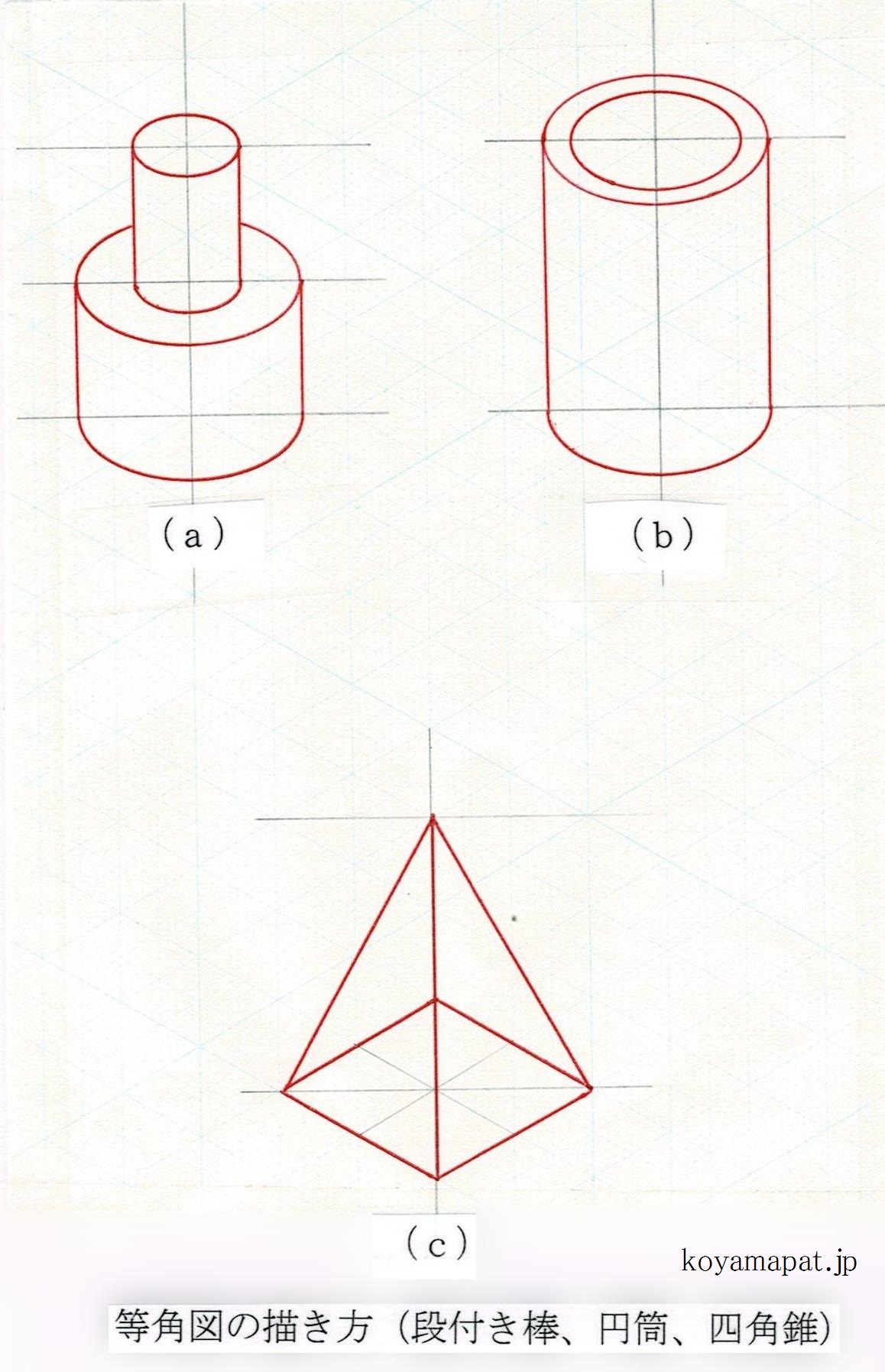
下図において、（ａ）は、直径２ｃｍ、高さ1.5ｃｍの大径部と、直径１ｃｍ、高さ1.5ｃｍの小径部とが連なった段付き棒です。（ｂ）は、内径1.5ｃｍ、外径２ｃｍ、高さ３ｃｍの円筒（パイプ）です。（ｃ）は、一辺が２ｃｍの正方形を底面とし、高さが３ｃｍの正四角錐です。底面が四角形以外の多角形でも、各角の座標が分かれば、同様に図示できます。

等角図の描き方（段付き棒、円筒、四角錐）

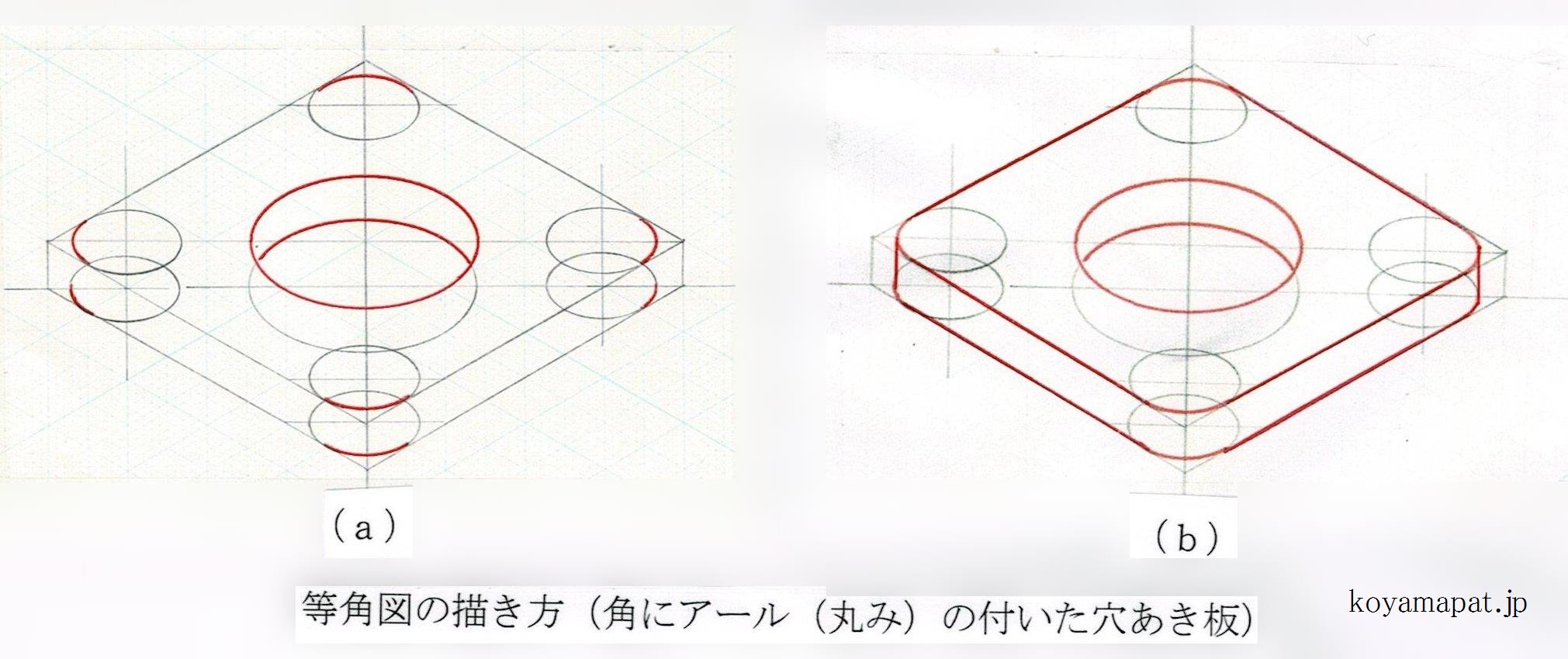
穴あき板

角にアール（丸み）の付いた穴あき板は、下図のように描くことができます。ここでは、一辺が４ｃｍで厚さ0.5ｃｍの四角形の板材で、中央部には直径２ｃｍの貫通穴があいています。また、板材の四隅は、半径0.5ｃｍの円弧で、丸みを付けられています。

等角図の描き方（角にアール（丸み）の付いた穴あき板）

等角図の作図方向（見る方向）

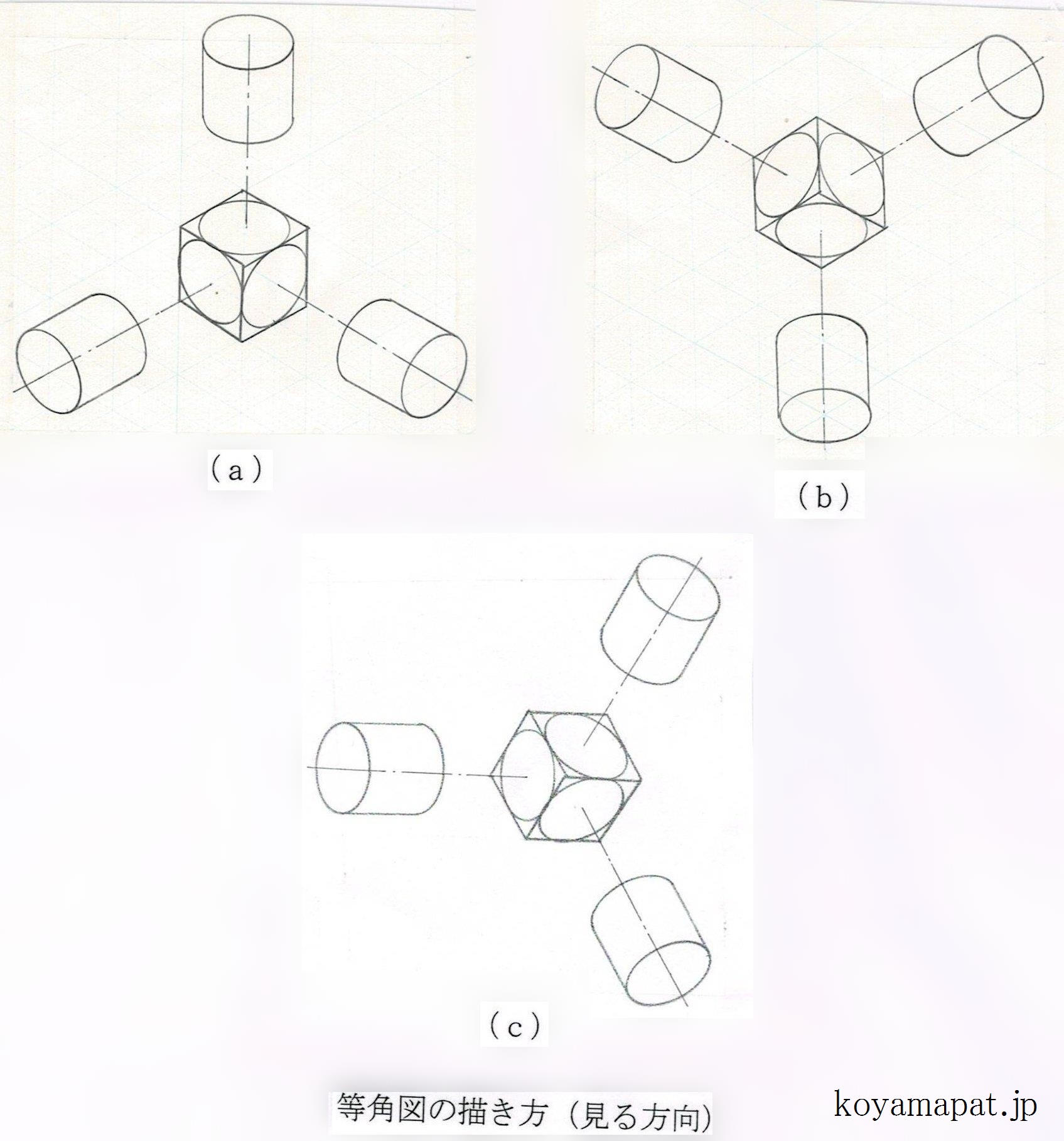
座標軸の配置

物体の底部や側部を中心に図示したい場合もあります。下図において、（ａ）は斜め上方から見た図、（ｂ）は斜め下方から見た図、（ｃ）は側方から見た図となります。（ａ）の図を回転させたものが（ｂ）や（ｃ）ということもできます。

等角図の描き方（見る方向）

様々な方向からの図示

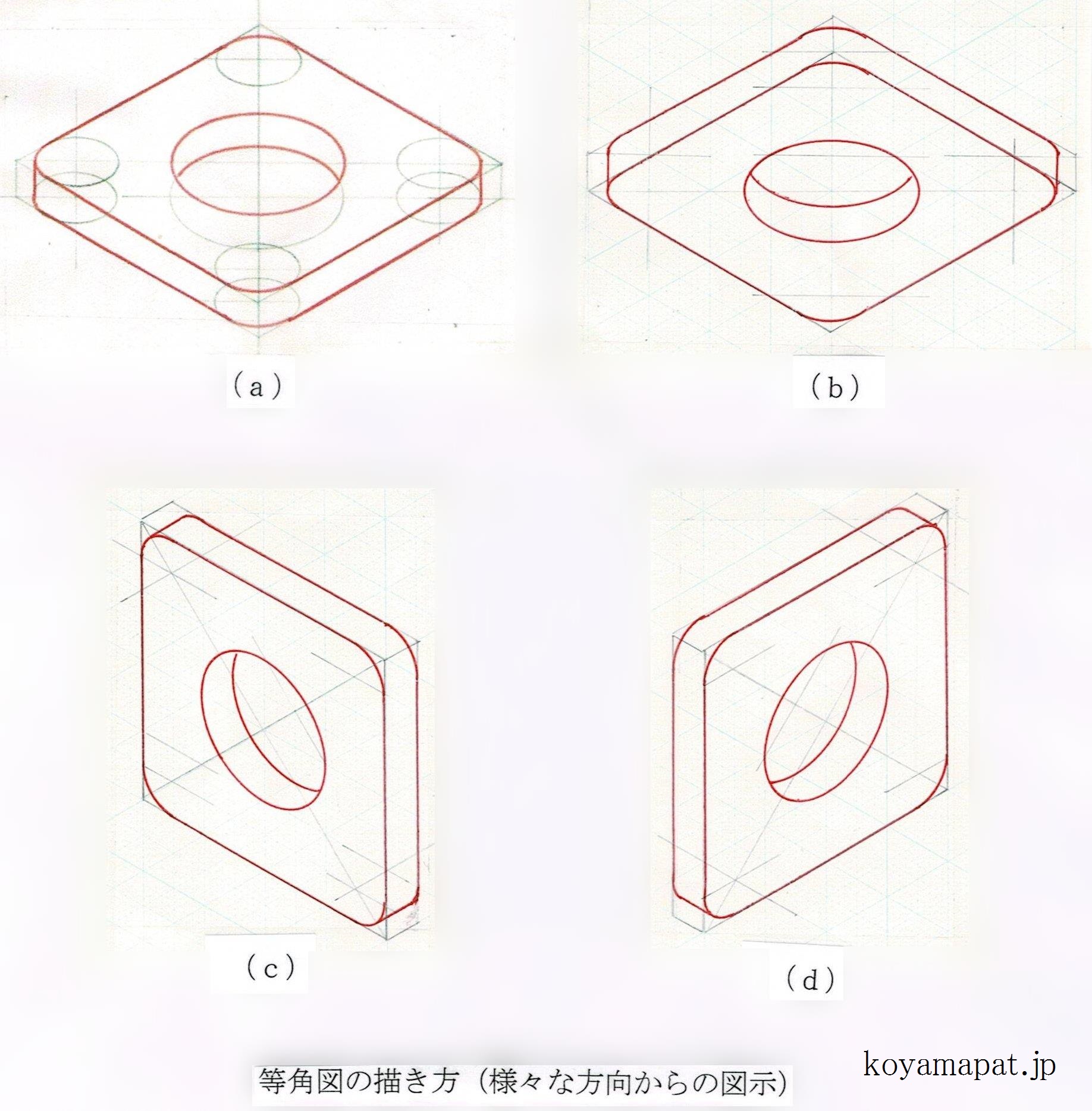
角にアール（丸み）の付いた穴あき板を、様々な方向から描いてみます。下図において、（ａ）は上方から見た図、（ｂ）は下方から見た図、（ｃ）は左側から見た図、（ｄ）は右側から見た図となります。

等角図の描き方（様々な方向からの図示）

最後に

特許出願用の図面では、斜視図が必要になることもあります。特許業界では、図面作成を専業でお仕事されている方もいらっしゃいます。

プロの手を借りなければ、難しいことも多いですが、発明者様との打合せなど、最低限の知識は必要と思われます。日々精進です。

目次