等角図と等角投影図 – 小山特許事務所

等角図（等測図）と等角投影図（等測投影図）との違いは、何でしょうか？

どちらのどの箇所が実寸？、0.82倍？、1.22倍？・・・

等角図と等角投影図との共通点と相違点をまとめてみます。

なお、等角図は等測図と呼ばれることもあり、等角投影図は等測投影図と呼ばれることもあります。

等角図と等角投影図の共通点

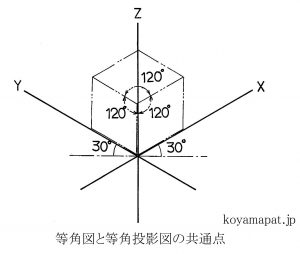
等角図も等角投影図も、いずれも、物体を斜め上方等から見た斜視図であり、前後、左右、上下の３本の座標軸（等角軸）が互いに等角（１２０度）で配置された図です。

両者の違いは、等角軸の軸方向寸法を実寸とするか否かです。

物体を所定に傾けると、物体は所定に縮小して見えることになり、その縮小状態を示す図が「等角投影図」です。一方、図面作成の便宜上、実寸を用いて作成されるのが「等角図」です。

以下、等角図と等角投影図との違いについて、具体的に見ていきます。

等角図と等角投影図の違い

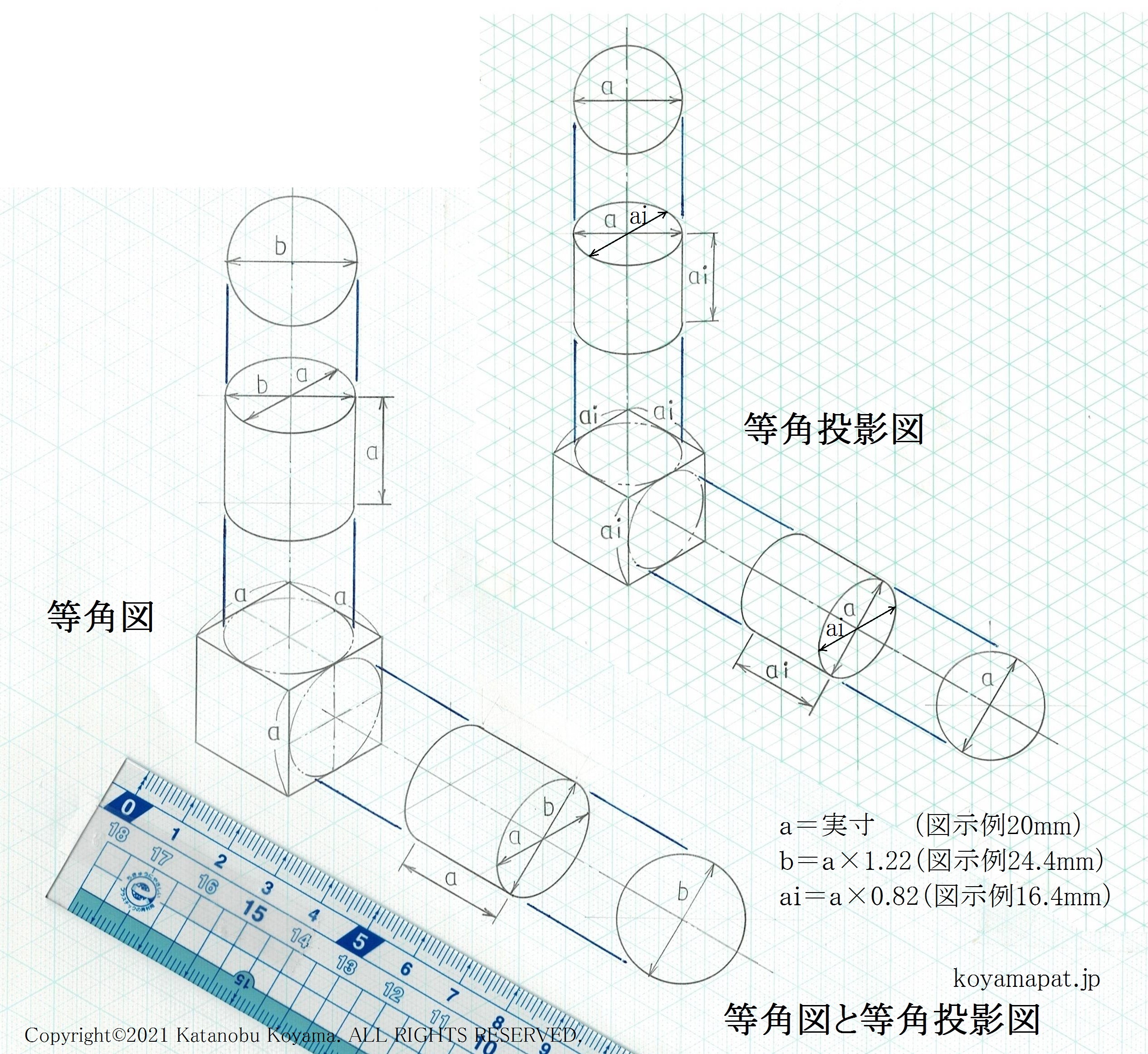
上図は、立方体、円柱および球を、等角図と等角投影図とで描いたものです。

いずれも、立方体は一辺が２０ｍｍ、円柱は直径が２０ｍｍで長さが２０ｍｍ、球は直径が２０ｍｍのものを描いています。

図中、ａが実寸、ｂがａの1.22倍（√３／√２）、ａｉがａの0.82倍（√２／√３）となっています。
つまり、ａ＝実寸、ｂ＝ａ×1.22、ａｉ＝ａ×0.82 です。

そのため、図示例では、ａ＝20mm、ｂ＝20×1.22＝24.4mm、ａｉ＝20×0.82＝16.4mm となっています。

なお、「ｉ」の付いた数値は、アイソメ尺（アイソメトリック縮み尺）での数値、つまり「実寸×0.82」であることを示しています。アイソメ尺のスケール（物差し）も市販されています。

いずれにしても、等角図と等角投影図とは、大きさの違い、ということになります。

等角図の描き方については、「斜視図（等角図）の描き方」をご覧ください。そして、寸法の取り方が異なるだけで、等角投影図についても同様に描くことができます。

等角図と等角投影図との違いをまとめますと、以下のとおりです。

なお、下記において、等角軸については、「等角図とは？」をご覧ください。
また、楕円の長軸や斜軸については、「楕円の長軸・短軸・斜軸とは？」をご覧ください。

等角図とは、物体を斜め上方等から見た斜視図であり、前後、左右、上下の３本の座標軸（等角軸）が互いに等角（１２０度）で配置された図で、かつ等角軸の軸方向寸法を実寸とした図をいいます。

等角投影図とは、物体を斜め上方等から見た斜視図であり、前後、左右、上下の３本の座標軸（等角軸）が互いに等角（１２０度）で配置された図で、かつ等角軸の軸方向寸法を実寸の0.82倍（√２／√３）とした図をいいます。