コンパスによる楕円の描き方

コンパスで楕円を描ける！？

斜視図（等角図）の描き方、等角図と等角投影図で見たように、等角図では３５度の楕円が用いられます。

楕円定規（テンプレート）がない場合、コンパス（または円定規・テンプレート）を用いて、楕円を作図することになります。

コンパスによる近似楕円の作図方法のうち、最も一般的で簡単と思われる方法をご紹介いたします。

まず、３５度楕円定規による作図がどのようなものか確認した後、コンパスによる作図方法を見ていきます。

本ページの解説動画：コンパスによる楕円の描き方【動画】

３５度楕円定規（テンプレート）による作図

楕円の描き方は、斜視図（等角図）の描き方、特に円柱や円錐の描き方にてご紹介のとおりです。

なお、下記において、等角軸については、等角図とは？をご覧ください。
また、楕円の長軸・短軸・斜軸については、楕円の長軸・短軸・斜軸とは？をご覧ください。

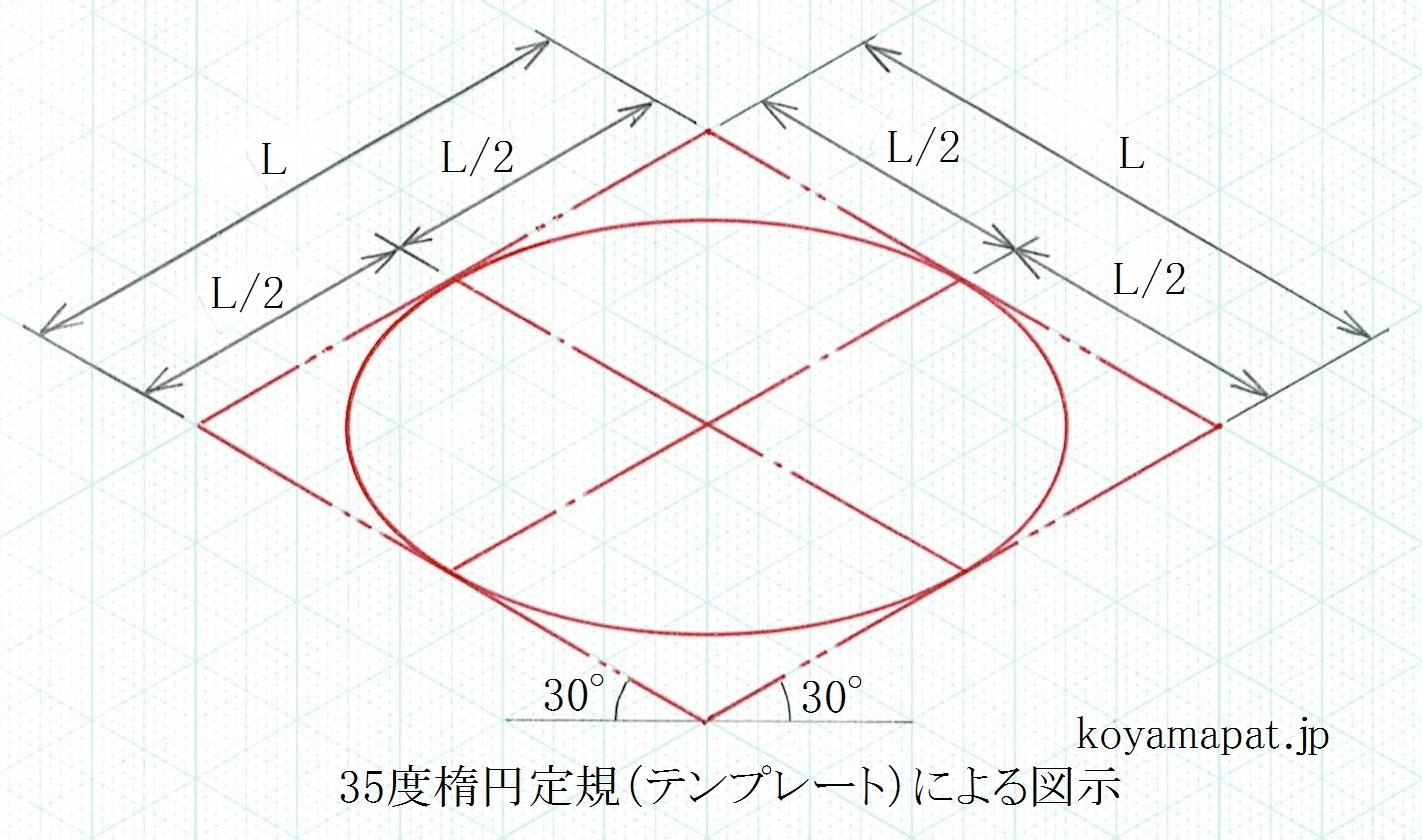
35度楕円定規（テンプレート）による図示

上図は、３５度楕円定規（テンプレート）により、直径Ｌ（図示例では５ｃｍ）の楕円を描いた図（等角図）です。

楕円は、一辺の長さがＬの四角形（等角図上では菱形）に内接します。この四角形の各辺は、水平線に対し３０度の傾きの線（等角軸に平行な線）となります。また、楕円の長軸は、前記水平線と平行な方向に配置され、楕円の短軸は、その水平線に対し垂直な方向に配置されます。そして、楕円の斜軸は、四角形の各辺と平行に配置され、この斜軸寸法は、円の直径として実寸Ｌとなります。さらに、四角形の各辺の中点において、楕円と四角形とが接します。

従って、次の点が分かります。

円の直径は楕円の斜軸寸法Ｌで実寸となる。
直径寸法Ｌを一辺とする四角形内に、楕円が内接する。
四角形と楕円との接点は、四角形の各辺の中点となる。

これに基づき、下記のとおり、楕円定規を用いないで、コンパス（または円定規・テンプレート）で楕円（近似楕円）を描くことができます。

コンパスによる近似楕円の作図

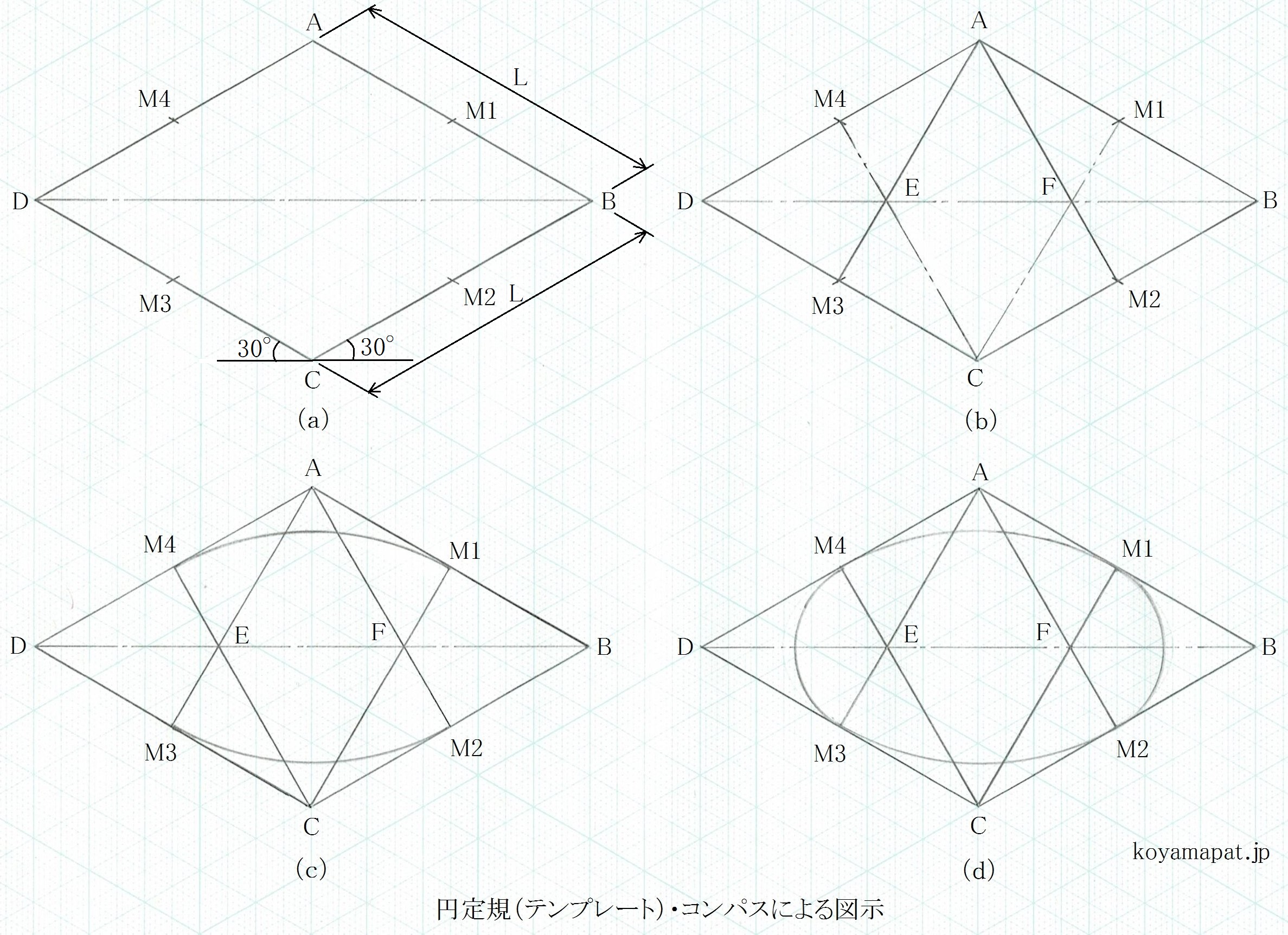
コンパスによる楕円の作図・図示

（ａ）まず、直径Ｌ（図示例では５ｃｍ）と対応した寸法を一辺とする四角形（菱形）を等角図で描きます。四角形の各辺は、水平線に対し３０度の傾きの線（等角軸に平行な線）となります。そして、各辺を二等分する箇所として、各辺の中点Ｍ１～Ｍ４も求めます。

（ｂ）頂点Ａと中点Ｍ２，Ｍ３とを線でつなぎます。同様に、頂点Ｃと中点Ｍ１，Ｍ４とを線でつなぎます。これら線は、頂点Ｄと頂点Ｂとを結んだ線上で交差し、交点Ｅ，Ｆを求めることができます。

（ｃ）頂点Ａを中心として、半径をＡ－Ｍ２（Ａ－Ｍ３）とする円弧を、中点Ｍ２とＭ３との間に描きます。同様に、頂点Ｃを中心として、半径をＣ－Ｍ４（Ｃ－Ｍ１）とする円弧を、中点Ｍ４とＭ１との間に描きます。

（ｄ）交点Ｅを中心として、半径をＥ－Ｍ３（Ｅ－Ｍ４）とする円弧を、中点Ｍ３とＭ４との間に描きます。同様に、交点Ｆを中心として、半径をＦ－Ｍ１（Ｆ－Ｍ２）とする円弧を、中点Ｍ１とＭ２との間に描きます。

このようにして、楕円定規を用いなくても、コンパス（または円定規・テンプレート）を用いて、近似楕円を描くことができます。

コンパスによる図示と楕円定規による図示との比較

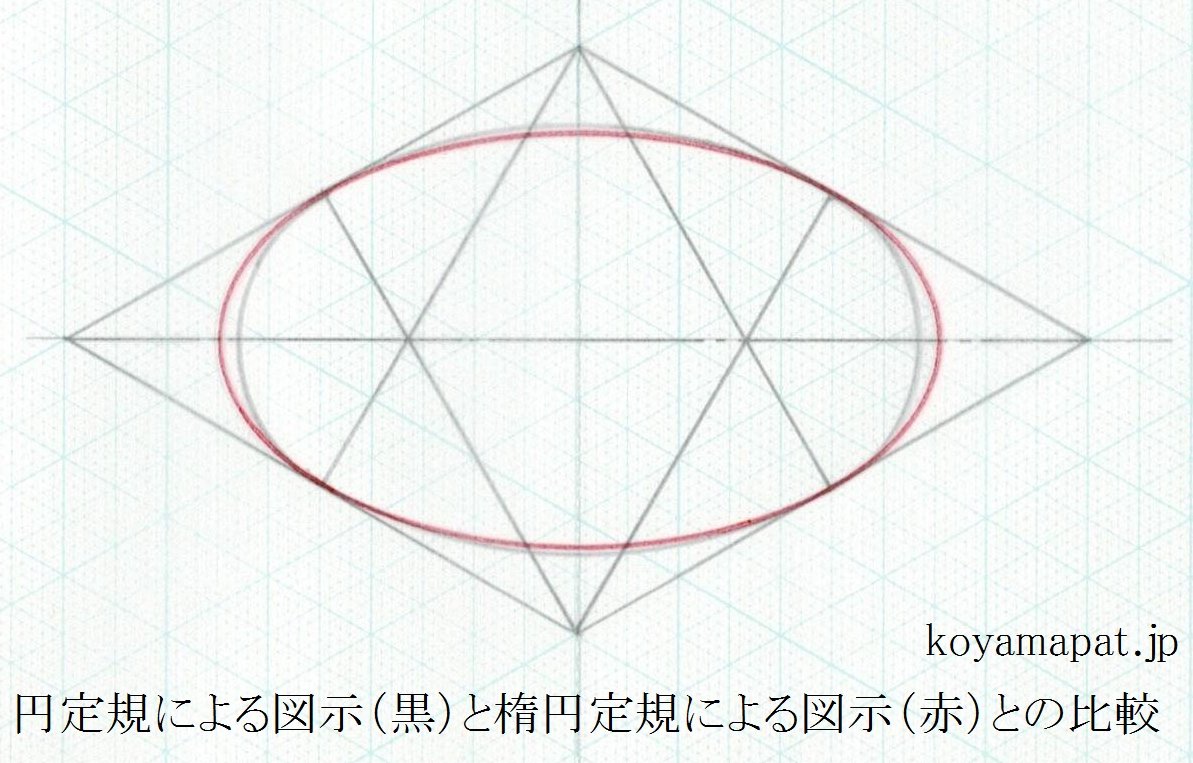
上図において、黒線は、コンパスを用いた近似楕円を示し、赤線は、３５度の楕円定規（テンプレート）による楕円を示しています。

両者に若干のズレはあるものの、円弧で近似楕円を描けていることが分かります。

コンパスで楕円を描ける！？

３５度楕円定規（テンプレート）による作図

コンパスによる近似楕円の作図

コンパスによる図示と楕円定規による図示との比較

関連情報